School of Mathematics & Statistics

Arithmetic Geometry

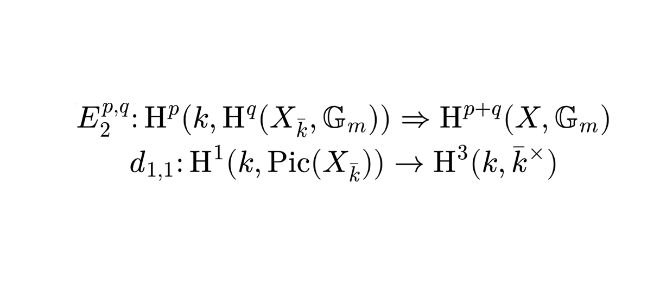
Arithmetic geometry is the study of algebraic varieties over non-algebraically closed fields. Such varieties exhibit many rich phenomena that entangle the geometric properties of the variety with the arithmetic properties of its ground field in a non-trivial way. One example are cohomological invariants like Brauer groups, which are fairly well-understood over algebraically closed fields but become more mysterious in the arithmetic setting, especially in higher Kodaira dimensions. In Glasgow, one focus of our group is the development of new cohomological techniques that enable us to determine these arithmetic invariants.